Learning to communicate about shared procedural abstractions
June 27, 2021
Learning to communicate about shared procedural abstractions seems like another confirmation of learning being a form of compression. Leans on Convention formation in iterated reference games. Humans use more efficient contextualized language to chunk useful concepts. GitHub repo.
Setup
98 humans paired up for a collaborative assembly task in 12 trials. Given a target scene architect instructs (up to 100 chars/turn) builder how to create that scene from some basic building blocks. Each scene consist of two towers (repeated across experiments); each tower of 4 dominoes. Tower types: (1) an arch, (2) “C”-shaped, and (3) “L”-shaped. After each trial, both participants see feedback about scene mismatch.
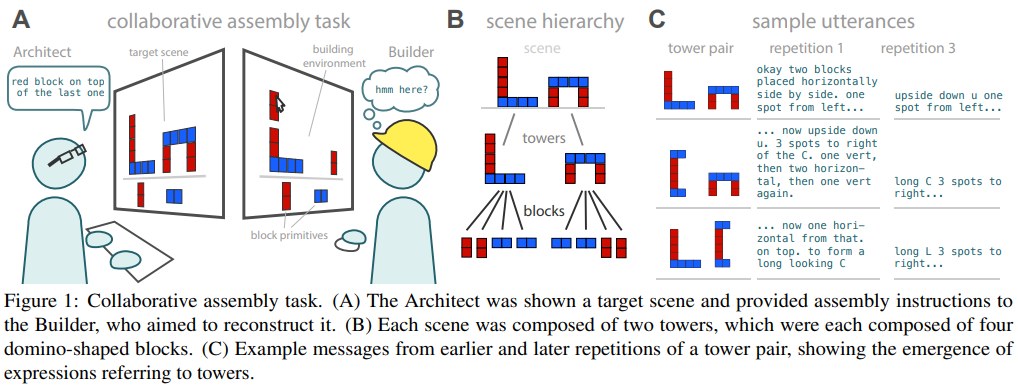
Eval
Start and final word distributions compared using permutation-based \(\chi^2\). As trials progressed, words like “block” and “horizontal” were used less frequently, while “C” and “shape” more frequently.
Linear Mixed Effects (x = repetition number) models show gain in efficiency.
Comparison between (architect, builder) pairs using Jensen-Shannon divergence (JSD) within each repetition. Interestingly JSD between pairs increases with trial number; i.e. a diverse language emerges even in this simple domain.
Computational model
The Architect must (1) have an underlying representation of the procedure they intend to communicate, (2) maintain uncertainty about whether the Builder is likely to share that representation, and (3) prefer shorter message over longer messages, all else being equal […] as the Architect becomes more confident that their abstracted referring expressions will be interpreted correctly, they increasingly prefer more efficient descriptions.
Bayesian program learning
Each agent maintains a library of primitives \(L\) to be combined; initialized with: \(h\) (horizontal), \(v\) (vertical), \(l\) (move left), \(r\) (move right) and digits \(1-9\). Trials of tower scenes designated \(\{T_n\}_1^N\). The model proposes a set of candidate sub-routine fragments \(f\) after each trial and updates a posterior over possible ways of extending the library:
\[P(L \cup \{f\} | \{T_n\}_1^N) \propto \underbrace{P(L \cup \{f\})}_{\textrm{description-length prior}} \cdot \underbrace{\prod_{n=1}^N P(T_n|L \cup \{f\})}_{\textrm{likelihood}}\]The likelihood captures the ability of an extended library efficiently to explain previous towers:
\[P(T_n | L \cup \{f\}) = \exp \left \{ -\textrm{MDL}(T_n | L \cup \{f\}) \right \}\]The prior captures a preference for smaller libraries:
\[P(L\cup \{f\}) = \exp \left\{ -w \cdot \textrm{size}(L \cup \{f\}) \right\}\]Communication as social reasoning
Following recent work, they model emergent language according to social utility. E.g. Pragmatic Language Interpretation as Probabilistic Inference:
Building on developments in game theory and probabilistic modeling, we describe the rational speech act (RSA) framework for pragmatic reasoning. RSA models provide a principled way to formalize inferences about meaning in context; they have been used to make successful quantitative predictions about human behavior in a variety of different tasks and situations, and they explain why complex phenomena, such as hyperbole and vagueness, occur. More generally, they provide a computational framework for integrating linguistic structure, world knowledge, and context in pragmatic language understanding.
Utterance step \(t_i\), procedural sequence \(T\).
\[P_s(u|t_i) \propto \exp\{-\alpha U(u;t_i)\}\] \[U(u;t_i) = \log P_l(t_i|u)\] \[P_L(t_i|u) \propto \delta_{u}(t_i)\]Delta is the literal meaning function that the Builder is expected to use. Architect can represent the raw scene \(T*\) using multiple programs \(T^k\):
\[U(u, T^k; T*) = \left ( (1-\beta) \sum \ln P_L(t_i^k | u) \right ) - \left ( \beta \cdot |T^k| \right )\]Where β is a parameter controlling the architect’s cost sensitivity, i.e. how much weight do they put on description length. The Builder may not know Architect’s language, so the Architects maintains an additional prior \(P([[ u ]])\) of the builder agent’s lexicon \([[u]]\), cf. When redundancy is useful:
Rational theories of language use have come under attack [for failing to] account for the seemingly irrational overinformativeness of referring expressions. [We present a model] that treats speakers as agents that rationally trade off cost and informativeness of utterances.
Not clear what “roughly” means in:
intermediate values of β roughly reproduced the qualitative Architect behavior
Discussion
Future work
- Investigate sources of consistency and variability
- e.g. “C-shape”, “upside-down U”
- Investigate within-pair references to previous trials
- Refine learning algorithm to fit experimental results
- Collect realistic priors
- Investigate tasks where participants learn at different rates
They are currently implementing a SOTA Bayesian program learning algorithm that incorporates language into the learning procedure.